How to Calculate P-Value: A Step-by-Step Guide
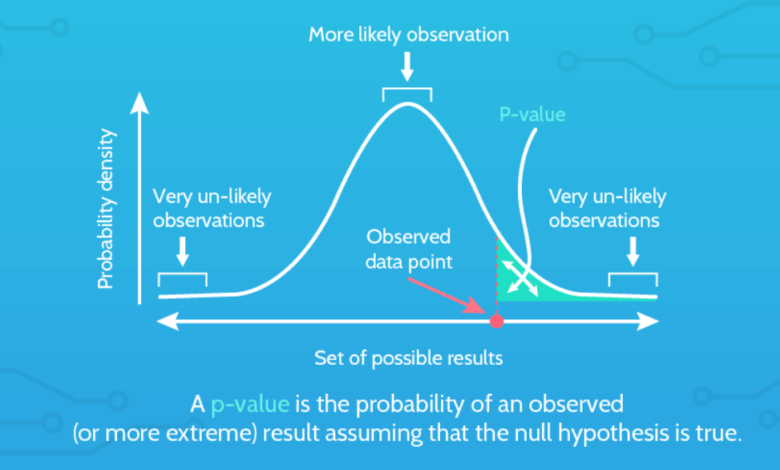
Statistical analysis plays a vital role in fields like science, economics, business, and healthcare. Among its key concepts, the p-value is one of the most frequently used indicators for determining whether an observed effect is statistically significant. While many rely on software to find p-values, understanding how to calculate p-value manually or conceptually is important for any student or professional working with data.
In this article, we’ll explore what a p-value represents, when it is used, and most importantly, how to calculate p-value using various statistical methods.
What Is a P-Value?
Before diving into the calculations, it’s essential to understand what a p-value tells us.
In simpler terms, a small p-value (usually less than 0.05) suggests that the observed data is unlikely under the null hypothesis, and therefore, we may consider rejecting the null in favor of the alternative hypothesis.
When Do You Calculate a P-Value?
You calculate a p-value when you are performing hypothesis testing. Some common scenarios include:
- Determining if a new drug has an effect.
- Testing whether a coin is fair.
- Checking if two groups have different averages.
Once you perform the appropriate statistical test (such as a t-test or z-test), the p-value helps you decide whether your findings are significant.
See also: Bo Nix Net Worth: College Football Star’s Earnings and NFL Potential
Step-by-Step: How to Calculate P-Value
Below are the most common methods with examples.
1. Using a Z-Test (for Large Samples)
The z-test is used when the population variance is known and the sample size is large (n > 30).
Steps:
Step 1: State your null and alternative hypotheses.
Step 2: Compute the z-score using the formula:
z=xˉ−μσ/nz = \frac{\bar{x} – \mu}{\sigma / \sqrt{n}}
Where:
- xˉ\bar{x} = sample mean
- μ\mu = population mean
- σ\sigma = population standard deviation
- nn = sample size
Step 3: Use the z-score to find the p-value from a standard normal distribution table or calculator.
Example:
A sample of 36 people has a mean height of 66 inches. What is the p-value?
Calculation:
z=66−652/36=12/6=3z = \frac{66 – 65}{2 / \sqrt{36}} = \frac{1}{2/6} = 3
Using a z-table, the p-value for z = 3 in a one-tailed test is about 0.0013.
For a two-tailed test, double it: 0.0026
2. Using a T-Test (for Small Samples)
The t-test is used when the sample size is small (n < 30), and population standard deviation is unknown.
Steps:
Step 1: Use the t-statistic formula:
t=xˉ−μs/nt = \frac{\bar{x} – \mu}{s / \sqrt{n}}
Where:
- ss = sample standard deviation
Step 2: Determine degrees of freedom (df): df=n−1df = n – 1
Step 3: Use a t-distribution table or calculator to find the p-value.
Example:
Sample size = 10, sample mean = 20, population mean = 18, sample standard deviation = 2
t=20−182/10=20.6325≈3.16t = \frac{20 – 18}{2 / \sqrt{10}} = \frac{2}{0.6325} \approx 3.16
df = 9
Looking up t = 3.16 with df = 9 in a t-table, the one-tailed p-value is around 0.006.
This indicates strong evidence against the null hypothesis.
3. Chi-Square Test (for Categorical Data)
Chi-square tests are used for evaluating observed vs. expected frequencies in categorical data.
Formula:
χ2=∑(O−E)2E\chi^2 = \sum \frac{(O – E)^2}{E}
Where:
- OO = Observed frequency
- EE = Expected frequency
Steps:
- Calculate the chi-square statistic.
Expected frequency = 10 for each face.
χ2=(10−10)210+(8−10)210+…=1.0\chi^2 = \frac{(10 – 10)^2}{10} + \frac{(8 – 10)^2}{10} + \ldots = 1.0
df = 6 – 1 = 5
Using a chi-square table, the p-value is approximately 0.96, meaning there’s no reason to reject the null hypothesis that the die is fair.
How to Calculate P-Value Using Software
In real-world scenarios, p-values are often computed using statistical tools:
1. Excel
Use functions like T.TEST, Z.TEST, or CHISQ.TEST
2. Python (using SciPy library)
from scipy import stats
p_value = stats.ttest_1samp([data], population_mean).pvalue
3. R Programming
t.test(data, mu = population_mean)
These methods save time and reduce calculation errors, especially for complex datasets.
Common Mistakes in Calculating P-Values
- Using the wrong test: Know when to use z-test vs t-test vs chi-square.
- Ignoring assumptions: Each test has conditions (e.g., normality, independence).
- Forgetting two-tailed vs. one-tailed difference: Always check which is appropriate.
Why P-Value Matters
Understanding how to calculate p-value is crucial in making informed decisions based on data. Whether you’re approving a new drug, testing business strategies, or conducting academic research, the p-value provides evidence that guides your conclusions.
It must be interpreted with context, confidence intervals, and understanding of the experimental design.
Conclusion
The p-value is a powerful tool for statistical inference. Knowing how to calculate p-value—either manually through formulas or by using software—enhances your analytical skills and helps you make evidence-based decisions. Whether you’re using a z-test for large samples, a t-test for smaller ones, or a chi-square test for categorical data, the logic remains the same: p-values help quantify how surprising your data is under the assumption of no effect.
By mastering this concept, you’ll gain deeper insight into research findings and improve your statistical literacy across multiple disciplines





